Sternevolutionsmodelle – eine kritische Betrachtung
Sonnenmodelle helfen dabei, die Sonne und die anderen Sterne, zu verstehen. Aus Modellrechnungen geht hervor, wie man sich die verschiedenen Phasen in der Existenz eines Sterns vorstellt. Zum Beispiel wie lange welche Phase der Existenz eines Sterns dauert und welches aller der Sterne daraus abgeleitet werden kann. Jedes Modell ist nur so gut wie seine Parameter. Neben messbaren Größen wie Außentemperatur, Helligkeit, Radius, Masse, Schwingungen, äußere chemische Zusammensetzung und Fusionsrate gibt es auch Modellannahmen. Dazu gehören zum Beispiel die ursprüngliche Rotation, die innere chemische Zusammensetzung, die innere Dichte sowie die Opazität oder Trübheit bzw. Durchsichtigkeit verschiedener chemischer Elemente. Hier wird ein Überblick über die Funktionsweise von Sonnenmodellen gegeben sowie über die Theorien, auf welchen die Modellannahmen beruhen, und es wird eingeordnet, wie gut diese jeweils empirisch belegt sind.
Ludmila Schneider (Stand 03.06.2025)
1. Einleitung
Sterne faszinieren den Menschen seit jeher. Allerdings existieren Sterne nicht unbegrenzt lange. Nach gängiger Theorie entstehen sie aus einer Gaswolke und durchlaufen dann verschiedene Stadien bis sie als Hüllenabstoß, oder Supernova bei großen Sternen, explodieren.1 Diesen Prozess nennt man Sternenevolution.
Anhand des sogenannten Hertzsprung-Russell-Diagramms (HR-Diagramm, siehe Abb. 1) und der Computermodelle ergibt sich ein vermuteter Werdegang. So entstehen Sterne gemäß der Theorie aus Gaswolken, die unter ihrer Gravitation kollabieren. Anschließend beginnt die Fusion von Wasserstoff zu Helium im inneren des Sternes. (Farag et al. 2020; Langer & Kudritzki 2014)
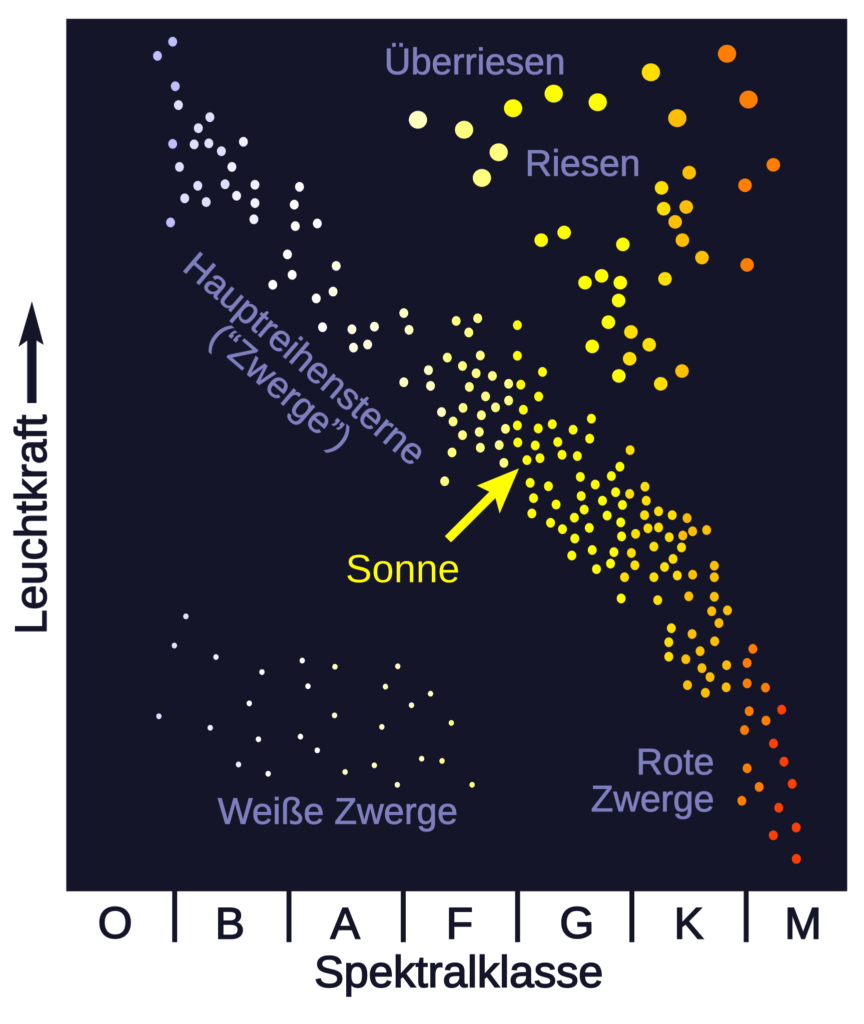
Abb. 1 „Dies ist ein Beispiel für ein Hertzsprung-Russell-Diagramm; ein Diagramm, das die Leuchtkraft einer Gruppe von Sternen in Abhängigkeit von ihrer Spektralklasse darstellt. Der diagonale Bereich mit der Bezeichnung „Hauptreihensterne“ ist der Bereich, in dem Zwergsterne wie die Sonne den größten Teil ihrer aktiven Lebenszeit verbringen. Rote Riesen und Überriesen sind weiterentwickelte Sterne mit einer größeren Masse als ein Roter Zwerg, die Elemente verbrennen, die schwerer als Wasserstoff sind. Weiße Zwerge hingegen sind recht dicht, leuchten nicht, haben aber immer noch eine geringere Masse als Überriesen. Wenn dieser Brennstoffvorrat erschöpft ist, wandern diese Sterne in diesem Diagramm nach links unten und werden zu Weißen Zwergen.“ (Sch – derived from Rursus, CC BY-SA 3.0, Wikimedia, https://de.wikipedia.org/wiki/Datei:HR-sparse-de.svg#/media/Datei:HR-sparse-de.svg)
Hierauf folgt die sogenannte T-Tauri Phase, bei der der junge Stern noch von Gas umgeben ist. Während dieser Phase ist der Stern noch instabil und erzeugt viele Ausbrüche (sog. Flares). Wenn der Stern sich irgendwann durch den Druck seiner Strahlung von diesem Gas befreit hat, beginnt die Main Sequence (Hauptreihe), bei der der Stern stabil Wasserstoff zu Helium fusioniert. Dies ist der längste Abschnitt im „Leben“ eines Sterns und auch der Zustand der heutigen Sonne. (Farag et al. 2020; Langer & Kudritzki 2014)
Wenn dann irgendwann der Wasserstoff im Kern verbraucht ist, wird das Helium zu Kohlenstoff, Sauerstoff und Stickstoff fusioniert und der Stern wird zum Roten Riesen. Im Laufe dieser Phase werden immer neue Elemente aus den Erzeugnissen der vorherigen Fusion fusioniert. Man nennt diese Phase deshalb auch Schalenbrennen. (Farag et al. 2020; Langer & Kudritzki 2014)
Dies geht so lange weiter, bis der Stern so ausgedehnt ist, dass seine Atmosphäre abgestoßen wird und zu einem Planetarischen Nebel wird. Der Kern des Sterns bleibt hierbei als Weißer Zwerg zurück. Bei großen Sternen geht die Fusion aber weiter, bis schließlich Eisen erzeugt wird. Nach dieser Fusion sind keine weiteren Fusionen mehr möglich und der Stern explodiert als Supernova. (Farag et al. 2020; Langer & Kudritzki 2014; Yusof et al. 2021)
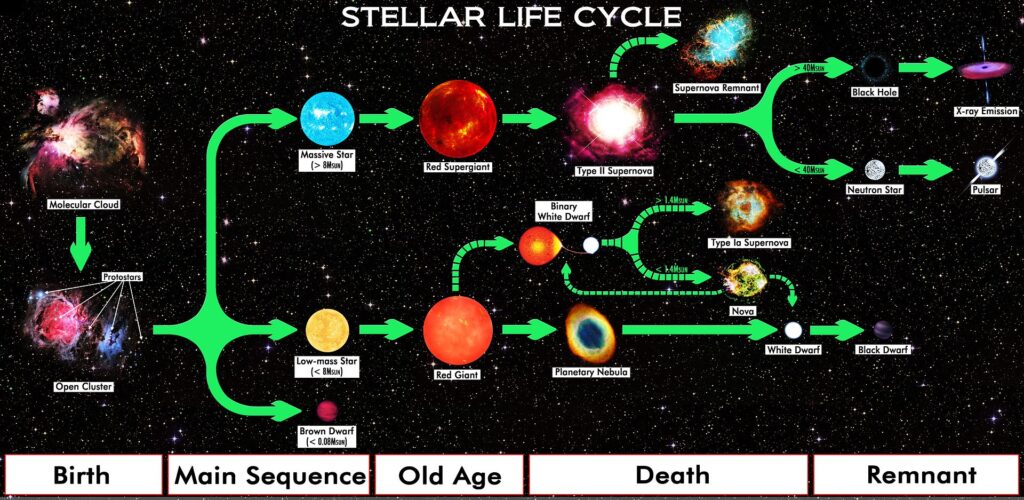
Abb. 2 Die Lebensphasen von Sternen nach theoretischen Berechnungen. (R.N. Bailey, CC BY 4.0, Wikimedia)
Auch wenn diese Entwicklungsschritte gut mit dem HR-Diagramm vereinbar sind, sind alle Übergänge fließend. Man kann also nicht wirklich sagen, wann eine Phase aufhört und wann die nächste beginnt. Zudem dauern die Phasen viel länger, als wir beobachten können. Somit können wir mit Ausnahme von Nova und Supernova nicht direkt beobachten, wie sich Sterne verändern. Wie lange also welche Phase braucht, und wie lange ein Stern insgesamt existiert, kann man nur mit Modellen berechnen und mithilfe der Sternhäufigkeitsverteilung im HR-Diagramm verifizieren. Diese Modelle werden in der Regel anhand unserer Sonne erstellt und anschließend auf alle anderen Sterne ausgedehnt. Somit sind Sonnenmodelle wichtig für unser Verständnis der Sternenevolution.
2. Modelle im Überblick
Grob betrachtet gibt es zwei Klassen von Sonnenmodellen. 1. Das „Module for Experiments in Stellar Astrophysics“ auch MESA genannt, ist zurzeit das Standardsonnenmodell. Gleichzeitig sind Wissenschaftler dabei, alternative Sonnenberechnungen zu erstellen. 2. Die Helioseismologischen Modelle, die anhand der Schwingungen der Sonne Vorhersagen über die Vergangenheit und Zukunft der Sonne treffen.
2.1 Die Grundparameter der Sonne
Beide Modelle (MESA und Helioseismologische Modelle) benötigen messbare Daten der heutigen Sonne als Grundparameter. Dies gilt insbesondere für die chemische Zusammensetzung der Sonnenoberfläche, die man sehr einfach anhand der verschiedenen Spektrallinien im Sonnenspektrum messen kann (Details unten). Hieraus berechnet sich die sogenannte Metallizität, also der Anteil an Elementen, die schwerer als Helium sind und in der Astrophysik als Metalle bezeichnet werden.
In der Regel wird hierzu der Eisenanteil durch den Wasserstoffanteil geteilt. Natürlich ist Eisen nicht das einzige Metall und man könnte die Metallizität auch aus der Summe der Anteile aller Elemente, die schwerer als Helium sind, geteilt durch den Wasserstoffanteil berechnen. Dennoch wird in den meisten Veröffentlichungen nur mit dem Eisenanteil gerechnet, da Eisen erst am Ende der Existenz eines Sterns entsteht und somit (laut Urknalltheorie) aus einem vorangegangenen Stern stammen muss, der als Supernova explodierte und dadurch das Material für einen neuen Stern lieferte. Somit hat man einen Vergleichswert für alle Klassen von Sternen. (Vinyoles 2017; Paxton et al. 2018; 2013, Jermyn et al. 2023)
MESA benötigt zudem auch noch folgende Parameter der Sonne:
- Radius
- Masse
- Helligkeit
- Radiometrisches Alter
- Fusionsrate
- Oberflächentemperatur
- Chemische Zusammensetzung der Oberfläche
Den Radius und die Helligkeit der Sonne kann man beobachten. Außerdem wird auch die Sonnenmasse über die Umlaufbahn der Erde und die Keplerschen Gesetze erhalten. Auch die Fusionsrate der Sonne ist aus Neutrinomessungen bekannt, wie in Abschnitt 4.4 erklärt wird. (Vinyoles 2017; Paxton et al. 2018; 2013; Wittkowski 2004; Jermyn et al. 2023)
Eine besondere Rolle spielt das radiometrische Alter des Sonnensystems von 4,6 Milliarden Jahren (Gyr). Weil man die Sonne selbst nicht radiometrisch datieren kann, werden Meteoriten mit der Uran-Blei-Methode datiert, woraus ein radiometrisches Alter des Sonnensystems errechnet wird. Dieses Alter ist einer der Grundparameter des MESA-Modells. (ebd.)
Im Gegensatz zu MESA benötigen Helioseismologische Modelle neben der chemischen Zusammensetzung der Oberfläche und der Metallizität auch Informationen über die Stärke und Geometrie des Magnetfelds der Sonne. Zudem werden aus den Schwingungen der heutigen Sonne die Tiefe der Konvektiven Zone (die Tiefe, bis zu der die Sonne noch flüssig genug ist, damit Blasen aufsteigen können, s. Abb. 3) als auch der Ort der Kernfusion im Inneren errechnet. (Anandaram 2014; Song et al. 2018; Christensen-Dalsgaard et al. 1991; Gizon & Birch 2012; Turck-Chieze et al. 2010)
2.2 Zu lösende Gleichungen
Leider sind nicht alle benötigten Größen der Sonnenmodelle messbar, weshalb kein Modell ohne Modellannahmen auskommt. So gehen alle Sonnenmodelle davon aus, dass die Sonne chemisch homogen ist und es immer war, dass sie also zu jeder Zeit und an jedem Ort die gleiche chemische Zusammensetzung hat. Das Entstehen neuer chemischer Elemente im Zentrum der Sonne wird hierbei als nicht signifikant angesehen. Diese Annahme kann man weder bestätigen noch widerlegen. Zudem müssen alle Modelle die Opazitäten oder Trübheiten verschiedener chemischer Elemente berücksichtigen, von denen es leider meist nur theoretische Werte gibt. Außer bei Eisen ist es bisher nicht gelungen, Opazitäten unter sonnenähnlichen Bedingungen in Labor zu messen. Außerdem wird der Materieverlust der Sonne, also Sonnenstürme und Flares, nicht berücksichtigt, da hierdurch keine starke Abweichung im Ergebnis erwartet wird. (Paxton et al. 2018; Wittkowski 2004; Badnell et al. 2005; Song et al. 2018)
Nicht alle benötigten Größen der Sonnenmodelle sind messbar, weshalb Modellannahmen benötigt werden – wie z. B., dass die Sonne immer chemisch homogen war.
MESA berücksichtigt der Einfachheit halber die Rotation der Sonne nicht. Dies ist aufgrund des Energiesatzes eine sinnvolle Annahme, da die Rotationsenergie der Sonne nur ein 0,00001-stel der Gravitationsenergie ausmacht. Allerdings erzeugt die Rotation den Sonnenzyklus von 11 Jahren und hat somit indirekt doch starke Auswirkungen. Zudem geht MESA davon aus, dass die Sonne eine perfekte Kugel ist, obwohl sie durch die Rotation an den Polen leicht abgeflacht ist. Auch die Erde ist durch die Fliehkräfte am Äquator ausgebeult und an den Polen abgeflacht. Man nennt diese Form einen Geoid. MESA berechnet außerdem die Sonne als Ideales Gas. Das heißt, dass sich alle Atome nur elastisch stoßen und nie aneinander hängen bleiben, ähnlich wie Billardkugeln. Diese Annahme hat allerdings aufgrund der großen elektrischen Abstoßung zwischen den ionisierten Atomen keine großen Auswirkungen auf die Berechnungen. (Paxton et al. 2018; 2013; Wittkowski 2004; Charbonneau 2014; Jermyn et al. 2023)
Helioseismologische Modelle benötigen hingegen Annahmen über die ursprüngliche Rotation der Sonne und ihre ursprünglichen Oszillationen oder Schwingung. Beide Größen kann man weder messen noch überprüfen und muss sie deshalb so wählen, dass am Ende die Berechnungen zu unserer Sonne passen. (Song et al. 2018; Capelo & Lopes 2020)
2.3 Zu lösende Gleichungen
In beiden Modellen müssen verschiedene zeitabhängige Gleichungen gelöst werden, um daraus ein Entwicklungsmodell der Sonne zu berechnen. In allen Modellen muss der Kollaps einer Gaswolke unter ihrer eigenen Gravitation modelliert werden, da dies laut unseren Modellen dem Anfang eines jeden Sterns entspricht. Außerdem müssen in allen Modellen thermodynamische Gleichungen gelöst werden, die die Zusammenhänge von Druck, Dichte und Temperatur beschreiben. (Paxton et al. 2018; 2013; Wittkowski 2004)
Eine wichtige Klasse an Gleichungen für MESA sind hydrodynamische und thermodynamische Gleichungen, die die Strömungen und Flüsse des Plasmas in der Sonne beschreiben. Besonders wichtig ist hier das hydrostatische Equilibrium (Gleichgewicht). Vereinfacht gesagt steht jeder Stern in einem stabilen Gleichgewicht, bei dem seine Gravitation von außen nach innen wirkt. Gleichzeit erzeugen die im Kern des Sterns entstehende Strahlung und Wärme einen immensen Druck von innen nach außen, der der Gravitation die Waage hält. Den Druck von Wärme kennen wir alle aus der Küche von überkochenden Töpfen und tanzenden Deckeln. Den Druck des Sonnenlichts spüren wir allerdings nicht. Da Licht bekanntlich sowohl Welle als auch Teilchen ist, hat es einen Impuls und kann Druck ausüben und damit zum Beispiel eine Lichtmühle antreiben. Was in unserem Alltag keine Rolle spielt, ist im Weltall, wo es weder Luftwiderstand noch Reibung gibt, ein wichtiger Faktor. Satelliten werden regelmäßig vom Sonnenlicht aus ihren Bahnen gedrückt und brauchen entsprechende Kurskorrekturen. (Jermyn et al. 2023)[1]
Für die Helioseismologie ist die Berechnung der Schallgeschwindigkeit im Sonneninneren von entscheidender Bedeutung. Die Schallgeschwindigkeit beschreibt, wie schnell sich Schwingungen und Wellen in einem Medium ausbreiten. (Song et al. 2018)
2.4 Technische Vereinfachungen und technischer Spielraum
Nun werden auf Basis dieser Gleichungen und Parameter Simulationen der heutigen Sonne durchgeführt. In der Regel laufen diese Simulationen in 1D, also in einer Raumdimension ab. MESA wurde zwar 2023 auf 3D erweitert, aber man kann davon ausgehen, dass die meisten Veröffentlichungen noch mit der alten Version berechnet wurden. Zudem sind alle Sonnenmodelle numerisch, das heißt, sie nähern sich dem Ergebnis in vielen kleinen Schritten an, statt es exakt analytisch zu berechnen. (Paxton et al. 2018; 2013; Song et al. 2018; Capelo & Lopes 2020; Jermyn et al. 2023)[2]
Zu diesem Zweck wird die Sonne in mehreren Zellen berechnet. Jede Zelle hat eine Tiefe, Breite und Länge. Außerdem hat jede Zelle ihre eigenen Parameter von Druck, Temperatur, Dichte und verschiedenen Koeffizienten. (Paxton et al. 2018; 2013) [3]
Die Größe der Zellen und der numerischen Näherungsschritte sind frei wählbar. Zudem bietet MESA die Option, die Schritte entweder in Zeit, Radius oder Masse zu berechnen. Grundsätzlich gilt: Je feiner die Schritte sind, desto mehr Details erhält man und desto mehr Zeit braucht eine Berechnung. Macht man allerdings die Schritte zu klein, konvergieren die Berechnungen nicht und man erhält gar kein Ergebnis. Stattdessen entsteht ein Effekt, den man als „numerisches Klingeln“ bzw. „numerische Instabilität“ bezeichnet. Vereinfacht gesagt macht der Computer dabei so viele kleine Schritte, dass er den Faden verliert und den Wald vor lauter Bäumen nicht mehr sieht. Er beginnt sich zum Beispiel um den wahren Wert herum zu drehen, ohne ihm dabei näher zu kommen. (Paxton et al. 2013; Jermyn et al. 2023)
Neben der Schrittgröße bieten helioseismologische Modelle die Möglichkeit, die Masse und Metallizität der Sonne zu variieren. MESA hingegen variiert den Anteil der Konvektion in % (wie viel Gas aufsteigen kann) und die Alpha-Mixing-Length, bei der das System quasi-adiabatisch ist. Die Größe Alpha beschreibt, wie groß das größte Stück der Sonne ist, das näherungsweise adiabatisch ist, also fast keinen Verlust von Energie und Materie nach außen hat. (Capelo & Lopes 2020; Paxton et al. 2013; Jermyn et al. 2023)[4]
Solche Berechnungen dauern in der Regel mehrere Stunden pro Durchlauf und müssen in mehreren Durchläufen gemacht werden. Deshalb geben sich Wissenschaftler große Mühe, mit Vormodellen und Vorberechnungen Zeit zu sparen. MESA wurde zum Beispiel im Jahr 2023 durch differenzielle Integrale optimiert. Das heißt, statt einer exakten Integration wird Zeit gespart, indem man über Grenzwerte sinnvolle Vereinfachungen findet. (Paxton et al. 2013; Jermyn et al. 2023)[5]
2.5 Ergebnisse
Am Ende der Berechnungen steht eine Simulation der heutigen Sonne sowie eine Berechnung ihrer Vergangenheit und eine Prognose ihrer Zukunft.
MESA erzeugt eine Sonne, die in Größe, Helligkeit und Masse der heutigen Sonne entspricht. Zudem berechnet MESA einen Verlauf von Temperatur und Kernfusion in der Vergangenheit und ein Profil von Temperatur und Dichte des Inneren der Sonne. Im Laufe der Zeit wurde das Modell auf andere Sterne erweitert und STELLA genannt. (Paxton et al. 2018; 2013][6]
Die verschiedenen Sonnen-Simulationen liefern Altersangaben zwischen 4 Gyr und 12 Gyr.
Helioseismologische Modelle liefern hingegen sehr unterschiedliche Simulationen der Sonne, die alle das Magnetfeld und die Schwingungen der heutigen Sonne haben und den gleichen inneren Aufbau. Sie liefern einen berechneten Helligkeitsverlauf der Sonne in der Vergangenheit. Zudem liefern sie verschiedene Alter zwischen 4,57 Gyr und 2,97 Gyr, die anhand des radiometrischen Alters von 4,6 Gyr überprüft werden. Sie unterscheiden sich allerdings um ein paar Prozent in Oberflächentemperatur, Radius und Helligkeit. Manche dieser Modelle werden für unsere Sonne ausgeschlossen. Allerdings werden manche Modelle, die wir für die Sonne ausschließen können, von Roten Riesen begünstigt. Dies weist auf Inkonsistenzen in den Modellannahmen und Parametern hin. Eine Erklärung könnte sein, dass die Opazitäten (Trübheiten) der chemischen Elemente in der Realität stark von den theoretisch berechneten Werten abweichen könnten. (Capelo & Lopes 2020; Bonanno & Fröhlich 2015)
Manche Modelle, die wir für die Sonne ausschließen können, werden aber von Roten Riesen begünstigt.
MESA gibt es übrigens kostenlos im Internet. Wenn man also Zeit, Muse und einen guten Computer hat, kann man den Code hier ausprobieren: https://docs.mesastar.org/en/latest/using_mesa/best_practices.html.
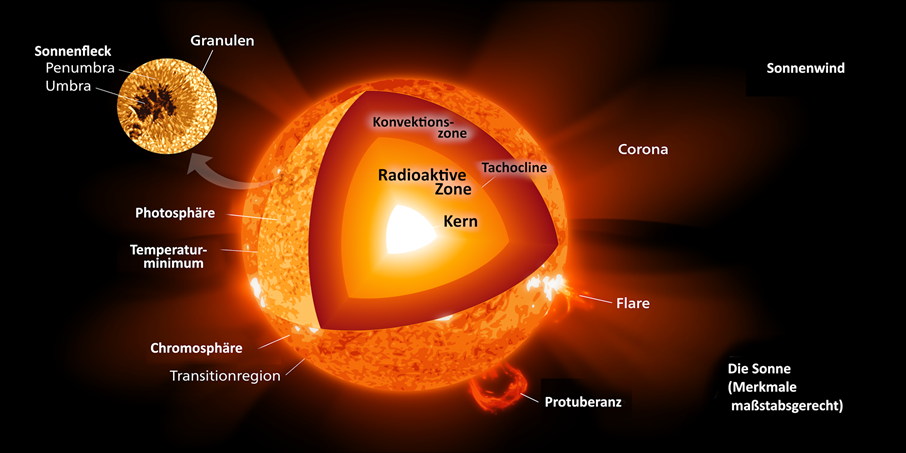
Abb. 3 Der innere Aufbau der Sonne. (B. Scholl nach Kelvinsong, CC BY-SA 3.0, Wikimedia)
3. Sind die Grundannahmen realistisch?
Die vereinfachende Annahme eines Idealen Gases, oder die Annahme, dass die Sonne exakt rund ist, hat nur wenig Einfluss auf die Berechnungen. Änderungen bei anderen Annahmen, haben jedoch große Auswirkungen. Zu diesen Annahmen gehören die chemische Zusammensetzung der Sonne und die Rotation, die trotz ihrer geringen Energie durch den Sonnenzyklus einen starken Einfluss hat. (Wittkowski 2004; Paxton et al. 2013)
3.1 Die Chemie des Sonnensystems
Die erste Grundannahme, die wir uns ansehen wollen, ist die chemische Homogenität. Diese Annahme hat mit der Theorie zur Entstehung des Sonnensystems zu tun.
Laut den gängigen Theorien entstand das Sonnensystem aus einer chemisch homogenen Gaswolke. Somit sind die Sonne, alle Planeten, alle Monde, alle Kometen und alle Meteoriten aus demselben Gas entstanden und müssten in etwa die gleiche chemische Zusammensetzung aufweisen. Einzige Ausnahme wären Objekte, die aus dem Weltraum von der Schwerkraft der Sonne oder eines Planeten eingefangen wurden und nun um die Sonne oder als Mond um einen Planeten kreisen. (Wittkowski 2004; Paxton et al. 2013; Jermyn et al. 2023)
Diese Annahme stimmt nicht mit Beobachtungen überein. Kometen bestehen zum größten Teil aus Wassereis, während Meteoriten als Eisen- und Gesteinsmeteoriten auftreten. Eisenmeteoriten bestehen fast ausschließlich aus Eisen und Nickel. Gesteinsmeteoriten hingegen bestehen aus Silikaten und Kohlenstoff, weshalb sie vor allem aus den Elementen Sauerstoff, Kohlenstoff und Silizium aufgebaut sind.[7]
Auch unsere Planeten weisen viele chemische Unterschiede auf. Wir kennen zum Beispiel Gasriesen wie Jupiter, Neptun, Saturn und Uranus, aber andererseits auch Gesteinsplanten wie die Erde, Merkur, Mars und Venus. Auch unter den Monden haben wir einerseits Eiswelten wie Europa und Phöbe, andererseits Gesteinskörper wie Ganymed, Callisto und unseren Mond oder auch Io, dessen Oberfläche fast ausschließlich aus Schwefel besteht, und Titan, der für seine dichte Gashülle bekannt ist.[8]
Laut den gängigen Theorien entstand das Sonnensystem aus einer chemisch homogenen Gaswolke, dennoch weisen Planeten und Meteoriten ganz verschiedene Zusammensetzungen auf.
Man versucht, diese Unterschiede mithilfe der sogenannten Frostlinie zu erklären, d. h. des Orbits innerhalb dessen die Temperaturen (durch die Nähe zur Sonne) so hoch sind, dass Wasser flüssig vorkommt. Weiter draußen im Sonnensystem gefrieren Wasser, CO2, Ammoniak, Methan und andere Substanzen zu Staubkörnern.[9] In unserem Sonnensystem liegen die Gesteinsplaneten innerhalb und die Gasriesen außerhalb der Frostlinie. Deshalb geht man davon aus, dass das Vorkommen von flüssigem Wasser, gasförmigem CO2, etc. die Planetenbildung beeinflusst hat. Allerdings gibt es durchaus viele Planetensysteme, die sogenannte heiße Jupiter beherbergen, also Gasriesen, die innerhalb der Frostlinie liegen und deshalb dieser Theorie widersprechen, falls sie nicht von außen nach innen gewandert sind. Es erstaunt wenig, dass Wissenschaftler anhand der großen chemischen Vielfalt der Planeten, Meteoriten und Monde davon ausgehen, dass sich in der anfangs chemisch homogenen Wolke, chemisch unterschiedliche Zonen gebildet heben. Dennoch wird angenommen, dass sich die Meteoriten der CI-Conditen-Gruppe chemisch nicht verändert haben und somit noch die Chemie der Ursprünglichen Gaswolke haben. (Lodders et al. 2025)[10]
Es ist einfach, die chemische Zusammensetzung der Sonnenoberfläche zu messen. Jede helle Linie im für uns sichtbaren Sonnenspektrum, sowie Linien in anderen Wellenlängen, wurde von einem anderen Element emittiert (ausgestrahlt, wie z. B. bei einer Lampe) und jede dunkle Linie wurde von einem anderen chemischen Element absorbiert („verschluckt“ so wie ein schwarzer Gegenstand das Licht im Raum „schluckt“). Da die Energiedifferenz zwischen den verschiedenen Schalen in der Atomhülle in jedem Element verschieden sind, können die Elektronen jedes Atoms andere Wellenlängen, also Farben, des Lichts emittieren oder absorbieren. So entsteht aus dem Muster der Linien im Sonnenspektrum eine genaue chemische Karte der Sonnenoberfläche. Ähnliche Messungen werden auch bei anderen Sternen, Galaxien und bei Planeten gemacht – und sind ziemlich zuverlässig.[11]
So sieht man, dass die Sonne (von außen) vor allem aus Wasserstoff, Helium, Stickstoff und Sauerstoff besteht. Zudem sind einzelne Moleküle wie Wasser, CO2 und Kohlenwasserstoffe nachweisbar. Allerdings sollten im Inneren der Sonne mit steigender Temperatur und Druck keine Moleküle mehr vorkommen.[12]
Bei schweren Spurenelementen wie Eisen, Magnesium und Calcium unterscheidet sich das Vorkommen in Meteoriten vom Vorkommen der Sonne um mehrere Promille. Dies stellt ein Problem dar, wenn die Sonne und alle Meteoriten aus derselben chemisch homogenen Gaswolke entstanden sind. Deshalb verwenden die Modelle für leichte Elemente wie Wasserstoff, Helium, Stickstoff und Sauerstoff die Vorkommen aus der Sonne, nämlich die Anteile des Elements geteilt durch den Anteil von Wasserstoff. Für die Anteile der schweren Elemente wie Eisen, Calcium und Magnesium fließen die Vorkommen aus Meteoriten in die Berechnungen der Sonnenmodelle ein. Diese Abweichung von mehreren Promille kann durchaus große Unterschiede ergeben, da vor allem helioseismologische Modelle stark von der Metallizität abhängig sind. (Wittkowski 2004; Paxton et al. 2013; Jermyn et al. 2023)
In den 1950er Jahren gab es Modelle, wonach der Kohlenstoffanteil der Sonne im Inneren steigt und die Sonne dadurch chemisch inhomogen werden könnte. Da wir heute allerdings wissen, dass die Sonne keinen Kohlenstoff erzeugt, wird in allen Modellen der Sonne chemisch Homogenität zugrunde gelegt. (Schwarzschild et al. 1957; Weymann 1957)
Ein Herabsinken schwerer Elemente unter die Sonnenoberfläche, wie man es bei anderen Sternen annimmt, schließt man für die Sonne aus, da diese gemäß den Theorien erst später in der Existenz eines Sterns auftreten. Genauso wird auch jede Umverteilung durch Fliehkräfte ausgeschlossen. Nach allen Modellen ist die Sonne homogen und war es auch immer. (Jermyn et al. 2023)
3.2 Das Problem mit der Opazität
Der Anteil verschiedener Elemente ist entscheidend – sowohl für die Ausbreitung von Wellen in der Sonne als auch für den Weg des Lichts nach außen. Aus den Raten der Absorption und Emission der verschiedenen Elemente wird die Opazität errechnet. Sie ist ein Maß für die Durchsichtigkeit eines Mediums. Ein dünner Nebel hat eine geringere Opazität als eine Regenwolke, da man die Sonne noch durch den Nebel erkennen kann.
Auf seinem Weg aus dem Inneren der Sonne nach außen hat ein Photon keine freie Bahn, sondern wird von zahllosen Atomen absorbiert und dann in eine beliebige Richtung emittiert. Auf diese Weise entsteht ein langer, chaotischer, völlig richtungsloser Weg, bis das Photon zufällig den Rand des Sonnenkerns erreicht und dann in der Konvektiven Zone mit heißem Gas aufsteigen kann. Deshalb benötigt ein Photon laut Modellrechnungen 10.000 bis 170.000 Jahre, um den Kern der Sonne zu verlassen (s. Abb. 4). Anschließend benötigt das Licht nur 75 Tage, um die Konvektive Zone zu durchqueren. (Mitalas & Sills 1992; Langer & Kudritzki 2014; Anandaram 2014)[13]
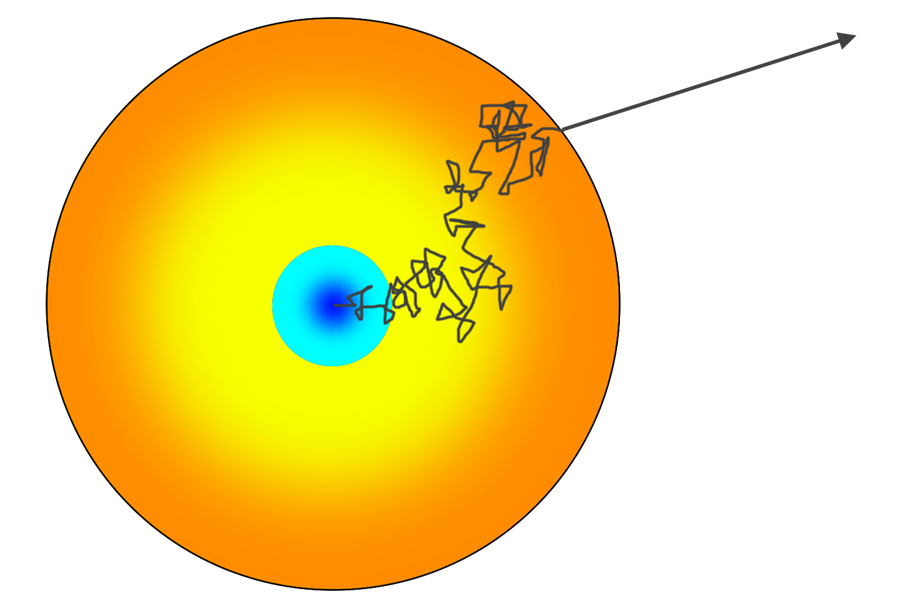
Abb. 4 Schematische Skizze des Wegs des Sonnenlichts durch die Sonne bis nach draußen (Skizze B. Scholl nach https://x.com/NASASTEM/status/1813202996739616944/photo/1)
Da das Photon auf seinem Weg so oft gestreut wird, ist dieser Weg und somit auch die innere chemische Zusammensetzung nicht mehr nachvollziehbar. Entsprechend lässt sich nur die chemische Zusammensetzung der Sonnenoberfläche messen, da das Photon danach in das Weltall entweicht und nicht von weiteren Atomen verändert wird.
Da Photonen auf ihrem Weg aus der Sonne heraus so oft gestreut werden, lässt sich nur die chemische Zusammensetzung der Sonnenoberfläche messen.
Der Weg und die Zeit, die ein Photon pro Schritt braucht, hängen stark von der Opazität und damit von der chemischen Zusammensetzung des Inneren der Sonne ab. Hier haben auch die kleinen Unterschiede zwischen der Sonne und den Meteoriten durchaus einen starken Einfluss, da im Sonnenkern Eisen, Neon und Magnesium den Hauptbeitrag zu der Opazität liefern, während es in der Konvektiven Zone vor allem der Sauerstoff ist. Würde es in der Sonne weniger schwere Elemente geben, würden sich Wellen in ihrem Inneren anders ausbreiten und Licht könnte schneller entweichen. Wenn es Zonen gäbe, wo weniger schwere Elemente anzutreffen sind, hätte das Licht auch solche Strecken, die es schneller bewältigen könnte. (Badnell et al. 2005; Anandaram 2014)
Wahrscheinlich würden sich, bei einer anderen inneren chemischen Zusammensetzung, auch die Berechnung der Tiefe der konvektiven Zone bei 71 % des Radius und des Ortes der Kernfusion und der Neutrinoproduktion ändern. Denn bei einer anderen Opazität, würden sich die Schwingungen in der Sonne anders ausbreiten. Auch würden sich die Schwingungen anders mit der Zeit verändern, was zu anderen helioseismologisch berechneten Altern führen würde. Diese Alter entstehen aus einer Rückberechnung der Schwingungen zu einer angenommenen ursprünglichen Schwingung und werden anhand des radiometrischen Alters von 4,6 Gyr überprüft. (Anandaram 2014; Christensen-Dalsgaard et al. 1991; Bonanno & Fröhlich 2015; Gizon & Birch 2012)
Bei einer anderen Opazität würden sich die Schwingungen in der Sonne anders ausbreiten und im Laufe der Zeit anders verändern, was zu anderen helioseismologisch berechneten Altern führen würde.
Wichtig ist zudem, dass die Opazitäten durch komplexe mathematische Funktionen beschrieben werden. Diese werden zur Vereinfachung nur in Abhängigkeit von Dichte und Temperatur berechnet. Die inneren Elektronen der Atome werden nicht berücksichtigt, da sie laut Modellrechnungen wenig Einfluss auf die Opazität haben. Gemessen wurde die Opazität unter sonnenähnlichen Bedingungen bisher nur bei Eisen, da solch hohe Drücke und Temperaturen schwer im Labor zu erzeugen sind. Die Messungen von Eisen haben alle bisherigen Theorien widerlegt. Tatsächlich ist die Opazität von Eisen 2- bis 4-mal höher als berechnet und erzeugt damit 25 % der Gesamtopazität der Sonne. (Badnell et al. 2005; Bailey et al. 2015; Hoarty et al. 2019)
Die Messungen von Opazität unter sonnenähnlichen Bedingungen bei Eisen haben alle bisherigen Theorien widerlegt.
Der Befund, dass die Opazität von Eisen alle Theorien für dessen Opazität widerlegt hat, legt die Vermutung nahe, dass noch mehr Elemente in Wirklichkeit andere Opazitäten haben könnten und dass sich so die Widersprüche zwischen den unterschiedlichen Sonnenmodellen auflösen könnten. (Song et al. 2018; Bonanno & Fröhlich 2015; Bailey et al. 2015; Hoarty et al. 2019)
3.3 Die rotierende Sonne – ein flüssiger Magnet
Eine weitere Modellannahme, die problematisch ist, ist die Tatsache, dass MESA die Rotation der Sonne nicht berücksichtigt. Zwar ist die Rotationsenergie der Sonne sehr gering, aber durch das Zusammenspiel von Sonnenrotation und dem Magnetfeld der Sonne über den sogenannten Dynamoeffekt entsteht der 11-jährige Sonnenzyklus. (Charbonneau 2014)
Tatsächlich kann ein komplexes Zusammenspiel aus Schwingungen und Magnetfeld das Alter der Sonne in helioseismologischen Modellen um bis zu 300 Millionen Jahre reduzieren. Bei anderen Sternen könnte dieser Effekt noch stärker sein. (Turck-Chieze et al. 2010)
Ein komplexes Zusammenspiel aus Schwingungen und Magnetfeld kann das Alter der Sonne in helioseismologischen Modellen um bis zu 300 Millionen Jahre reduzieren.
Nun besteht die Sonne aus ionisiertem (elektrisch geladenem) Gas, sogenanntem Plasma. Dieses Plasma rotiert, weil die Sonne rotiert. Wir wissen aus dem Alltag, dass dort, wo immer Strom fließt, Magnetfelder entstehen. Deshalb haben Kabel und Elektrogeräte ein Magnetfeld. Diese Magnetfelder werden aus den kleinen Feldern der fließenden Elektronen erzeugt. Und ebenso erzeugt das fließende Plasma das Magnetfeld der Sonne. Allerdings ist die Sonne flüssig und rotiert deshalb aufgrund der Trägheitskräfte an den Polen langsamer. (Charbonneau 2014)
Das führt dazu, dass das Plasma am Äquator das Plasma an den Polen überholt. Hierbei dehnt sich das Magnetfeld der Sonne und beult sich immer mehr aus, bis es sich letzten Endes selbst überholt, was zu einer komplexen Rückkopplung führt. Etwas Derartiges ist im Sommer 2024 passiert. In diesem Jahr hatte die Sonne ihre aktive Phase, weshalb viele Sonnenflecken sowie Sonnenstürme beobachtet werden konnten und dieses Jahr besonders viele Polarlichter auftraten. (Charbonneau 2014)
Anschließend baut sich das Magnetfeld neu auf, allerdings genau umgekehrt wie vorher. Das führt zu ruhigen Phasen im Zyklus. Eine solche Phase gab es vor sieben Jahren.[14] (Charbonneau 2014)
Deshalb beeinflussen die Rotation, das Magnetfeld und der dadurch entstehende Sonnenzyklus die Sonne stark. Es kommt zu zusätzlichem Energieverlust, Materieverlust und Vermischung. Bei jungen Sternen, die schnell rotieren, könnte dieser Effekt sogar noch größer sein. (Turck-Chieze et al. 2010; Bétrisey 2024)
Mittlerweile gibt es erste Modelle, die die Sonnenrotation berücksichtigen. In diesen Modellen macht eine langsame Anfangsrotation bzw. gar keine Anfangsrotation der Sonne nur wenig Unterschied. Eine Simulation ohne Anfangsrotation liefert aber Ergebnisse, die besser zur heutigen Sonne passen. (ebd.)
Tatsächlich finden in diesen Modellrechnungen sowohl bei schneller als auch bei langsamer Anfangsrotation ab dem Alter von 1 Gyr keine großen Veränderungen mehr statt. Zudem bleiben die Außenrotation und die Rate der pp-Kernfusion (der häufigste Fusionsvorgang von Wasserstoff zu Helium) ab einem Alter von 2 Gyr in der Simulation fast gleich, während die Rotationskurve der Kernrotation immer steiler wird. (ebd.)
Trotzdem eignen sich diese Simulation nicht als Indiz für eine junge Sonne (2 Gyr oder jünger), da die Helligkeit in der Simulation nach 2 Gyr nur bei 82 % der heutigen Sonnenhelligkeit liegt. (ebd.)
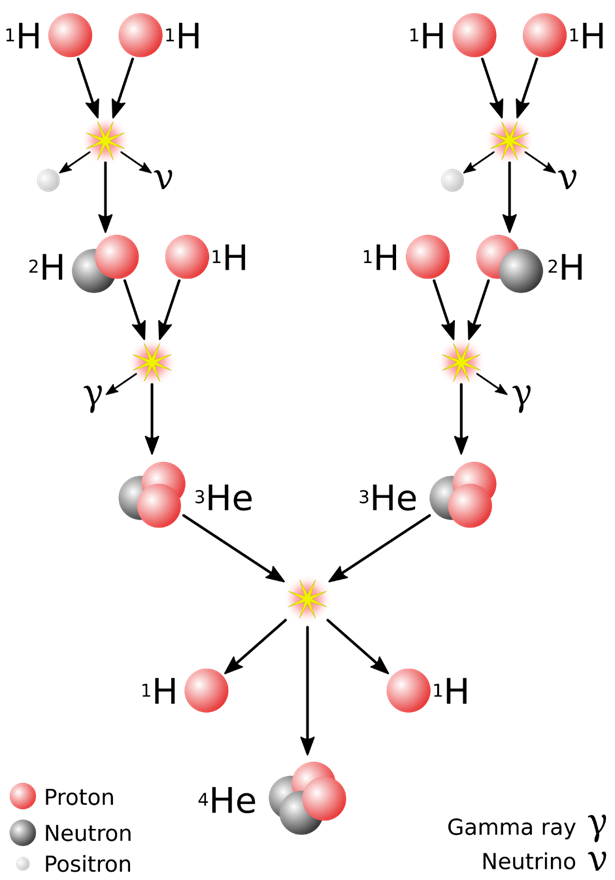
Abb. 5 Schema der Proton-Proton-Reaktion I (= pp-Zyklus). (Sarang, Public Domain, Wikimedia)
3.4 Die Neutrinos
Die äußere Temperatur der Sonne, ihre innere Temperatur als auch die Fusionsrate und die Art der Kernfusion sind wichtige Parameter der Sonnenmodelle. Die Sonne bekommt wie alle anderen Sterne ihr Licht aus Kernfusionen in ihrem Inneren. Diese Informationen werden mithilfe von Neutrinos gemessen. (Neutrinos sind Elementarteilchen, sogenannte Leptonen, so wie auch das Elektron ein Lepton ist.) Es gibt sie als Elektron-, Myon-, und Tau-Neutrinos. Überraschend ist, dass Neutrinos oszillieren, sich also mal in Elektron-, mal in Myon- und mal in Tau-Neutrinos verwandeln. (Haxton 1995; Smirnov et al. 2016)[15]
Für die Bestimmung der Fusionsrate ist vor allem das Elektron-Neutrino interessant, weil es am einfachsten zu messen ist, und Neutrinos in Kernfusionen als Elektron-Neutrinos entstehen.
Das Elektron-Neutrino lässt sich vereinfacht als neutrales Elektron betrachten. Es ist klein, elektrisch neutral und bewegt sich fast mit Lichtgeschwindigkeit. Nachweisen lässt es sich nur über die Schwache Wechselwirkung, wenn es zufällig mit einem Elektron oder Proton zusammenstößt. Anschließend kann das freigesetzte Elektron gemessen werden. Entsprechend können Neutrinos völlig ungehindert aus dem Inneren der Sonne entweichen. Sogar die Erde und auch jeder von uns wird pro Sekunde von Trilliarden von Neutrinos durchsiebt, ohne dass auch nur eines davon hängen bleibt oder irgendeinen Einfluss auf uns hat. (Bellerive 2004)[16]
Um Neutrinos zu messen, braucht man tonnenschwere Wassertanks wie in Borexino oder Superkamiokande um die schwach wechselwirkenden Teilchen einzufangen. Aus den Borexino-Messungen ergibt sich ein Fluss von 6,1 ± 0,6 * (1010 /cm2s). Aus den Sonnenmodellen wurden 5,97 ± 0,04 * (1010 /cm2s) Neutrinos erwartet. Das liegt im Bereich der Messfehler und folglich bestätigen die Borexino-Messungen die Theorie. (Bellerive 2004; Park 2001; Agostini et al. 2017; Smirnov et al. 2016)[17]
Tatsächlich können wir anhand der Energieverteilung der Neutrinos nachvollziehen, aus welchem Kernfusionsprozess sie stammen. Und an der Menge der jeweiligen Neutrinos kann man erkennen, wie häufig diese Fusion in der Sonne stattfindet. So können wir die Fusionen im Inneren der Sonne Schritt für Schritt nachvollziehen. Tatsächlich fusioniert die Sonne vor allem Wasserstoff zu Helium im sogenannten pp-Zyklus (siehe Abb. 5). Die Fusion von Kohlenstoff, Sauerstoff oder Stickstoff findet hingegen nicht statt, da Temperatur und Druck für diese Fusion nicht hoch genug sind. All diese Fusionsraten und damit auch der Fluss der Neutrinos hängen von der Kerntemperatur der Sonne ab und ermöglichen somit Rückschlüsse auf die Kerntemperatur. (Bellerive 2004; Bahcall & Ulmer 1996; Smirnov et al. 2016; Song et al. 2018; Salmon et al. 2021)[18]
Von anderen Sternen und ihren Fusionsprozessen wie zum Beispiel dem Schalenbrennen in Roten Riesen können wir leider nicht genügend Neutrinos messen. Somit haben wir nur Modellrechnungen dazu, was im Inneren von Roten Riesen stattfindet, da es keine experimentellen Nachweise gibt. Im Gegensatz dazu sind uns die Vorgänge und die Temperatur im Inneren der Sonne dank der Neutrino-Messungen gut bekannt. (Farag et al. 2020; Bellerive 2004; Yusof et al. 2021)
Von Fusionsprozessen in nicht-sonnenähnlichen Sternen können wir nicht genügend Neutrinos messen und sind daher auf Modellrechnungen angewiesen.
3.5 Woraus besteht das Sonnenlicht?
Natürlich erzeugen die genannten Kernfusionen nicht nur Neutrinos, sondern auch ein breites Spektrum an elektromagnetischer Strahlung, darunter sichtbares Licht, das wir als Sonnenlicht kennen. Hieraus lässt sich neben der chemischen Zusammensetzung der Sonnenoberfläche auch die äußere Temperatur der Sonne berechnen. Die Sonne leuchtet in jeder Wellenlänge, von Gammastrahlung, über Röntgenstrahlung, UV-Strahlung, sichtbares Licht, Infrarot, Mikrowellen und Radiowellen. Allerdings schützt uns unsere Erdatmosphäre vor aller Strahlung außer Infrarot, sichtbarem Licht und weichem UV, sodass uns die anderen Wellenlängen keinen Schaden zufügen können. Gleichermaßen schützt uns unser Magnetfeld vor Sonnenstürmen, heißem Plasma, geladenen Teilchen des Sonnenwinds und der Radioaktivität des Weltalls. (Russel 2007)[19]
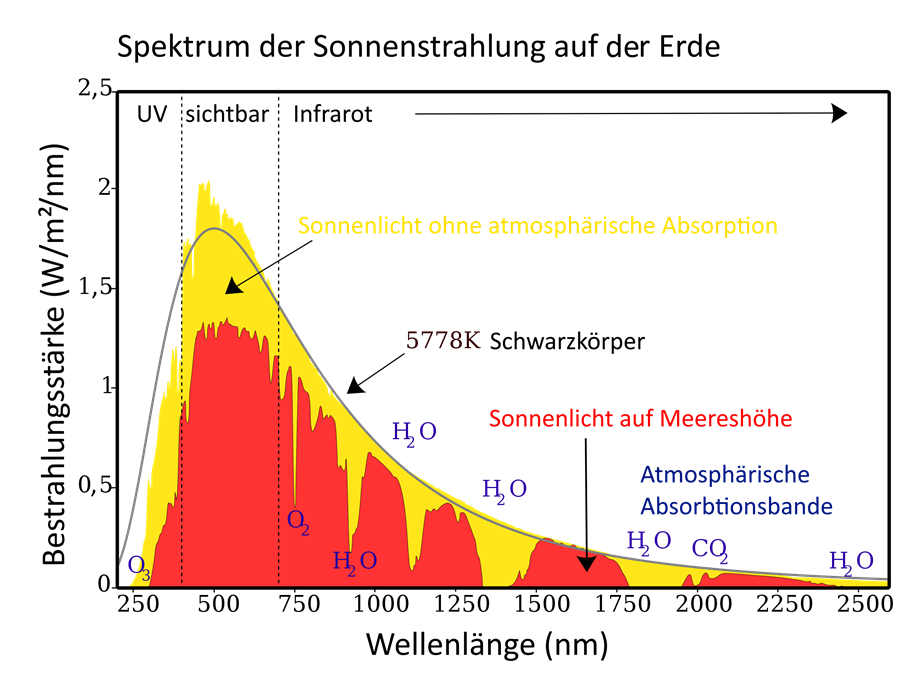
Abb. 6 Spektrum der auf der Erde eintreffenden Sonnenstrahlung. (nach Robert A. Rohde – extracted from another file, CC BY-SA 3.0, Wikimedia)
Wie schon erwähnt, sehen wir im Spektrum der Sonne viele helle Emissionslinien und dunkle Absorptionslinien, die uns auf die chemische Zusammensetzung der Sonne schließen lassen. Die Gesamtform des Sonnenspektrums entspricht einer Schwarzkörper-Kurve mit einer Temperatur von 5900 K (Kelvin entspricht Grad Celsius, orientiert sich aber am absoluten Nullpunkt von -273,15 °C; 5900 K = 5626,85 °C). Ein Schwarzkörper ist ein Objekt, dessen Strahlungskurve ausschließlich von der Temperatur abhängt. Auf diese Weise lässt sich die Außentemperatur der Sonne sowie auch die von anderen Sternen direkt messen. (Langer & Kudritzki 2014; Russel 2007)[20]
Somit sind sowohl die äußere Temperatur als auch die äußere chemische Zusammensetzung eines Sterns direkt messbare Parameter, die für unsere Sonnenmodelle verwendet werden können.
Die äußere Temperatur und die äußere chemische Zusammensetzung eines Sterns sind direkt messbare Parameter.
4. Ein kleiner Exkurs zur Uran-Blei-Methode
Zum Schluss soll kurz auf das radiometrische Alter der Sonne von 4,6 Gyr eingegangen werden. Dieses Alter ergibt sich aus der Uran-Blei-Datierung von Meteoriten. Uran zerfällt in 14 Schritten zu Blei. Jeder Schritt hat eine Halbwertszeit. Hieraus lässt sich die Gesamthalbwertszeit der ganzen Reihe berechnen (unter der Annahme, dass radioaktive Zerfälle immer gleich schnell vonstattengehen). Somit lässt sich aus einer Menge Blei zurückrechnen, wie lange es gedauert hat, dieses Blei zu erzeugen, wenn alles Blei einmal Uran gewesen sein sollte (was eine weitere Vorannahme ist). (Ehrmann 2019)
Bei Meteoriten nimmt man an, dass es weder zu Verunreinigung noch zu Stoffverlusten kommt. (Und natürlich, dass sie aus unserem Sonnensystem stammen und nicht viel früher irgendwo anders entstanden und dann von unserem Sonnensystem eingefangen wurden.) Meteoriten sind im Vakuum des Weltalls isoliert. Allerdings sind sie dort ebenfalls der vollen Weltraumstrahlung ausgesetzt. (Wittkowski 2004; Paxton et al. 2013)[21]
Zudem entstehen laut gängigen Entstehungstheorien Gesteine im Weltall dadurch, dass sich Staubkörner zusammenklumpen. Die körnige, granuläre Struktur von Gesteinsmeteoriten unterstützt diese Theorie. Entsprechend müssten die Wissenschaftler für die Annahme, dass Meteoriten nicht verunreinigt sind, ein Argument liefern, warum ab einem bestimmten Moment kein neuer Staub hinzukommt. Sonst würde es durch den Staub zu Verunreinigungen kommen. Staub, der nicht von der Zeit der Entstehung des Sonnensystems stammt, würde eine andere chemische Zusammensetzung haben.
Außerdem sind Zusammenstöße im Weltall zwar selten, laufen aber manchmal mit solcher Wucht ab, dass Gesteine schmelzen und Splitter wegfliegen. Entsprechend kann man, auch wenn Stöße im Weltall durchaus selten sind, hinterfragen, ob es realistisch ist, dass Meteoriten über einen Zeitraum von 4,6 Gyr keine Verunreinigungen erhalten haben. (Paxton et al. 2018; Wittkowski 2004; Badnell et al. 2005; Song et al. 2018)[22]
Leider gibt es für Meteoriten keine unabhängigen Altersbestimmungen. Da die Uran-Blei-Methode auch für die Gesteine verwendet wird, in denen Fossilien liegen, können dieselben Argumente für bzw. gegen beide Altersdatierungen verwendet werden. (vgl. Kotulla 2020)
Hinweise auf ein jüngeres Alter sind zum Beispiel die Funde von weichem Bindegewebe an Dinosaurierknochen, die auf 75 Millionen radiometrischer Jahre (und mehr) datiert wurden, oder lebende Bakterien, die in Steinen eingeschlossen waren, die 250 Millionen radiometrische Jahre alt sind. Dass weiches Gewebe 75 Millionen Jahre überstehen kann oder ob Bakterien 250 Millionen Jahre als Sporen überleben können, scheint unwahrscheinlich. (Bertazzo et al. 2015; Binder 2020; CBSNews.com 2000)
5. Weitere Beobachtungen, die problematisch sein könnten
Neben den bisher genannten Schwierigkeiten gibt es weitere Befunde, die ein Problem für Sternenevolutionsmodelle darstellen.
Rote Zwerge stellen die Wissenschaft vor ein Rätsel. Sie sind die kleinsten Sterne, in denen Wasserstoff zu Helium fusioniert. Wir kennen bereits viele solcher Objekte wie zum Beispiel Proxima Centauri. Rote Zwerge leuchten nur schwach, und sind zudem laut Computermodellen völlig konvektiv. Sie haben also keinen festen Kern, sondern bestehen nur aus einer konvektiven Zone. Auf diese Weise könnten Rote Zwerge ihre Kernfusion fortsetzen, bis das letzte Wasserstoffatom verbraucht ist. Deshalb ist die „Lebensdauer“ von Roten Zwerge laut den Modellberechnungen über 13,8 Gyr und damit älter als das Universum laut Urknallmodell. Erst danach würde ein Roter Zwerg zu einen Helium-Weißen-Zwerg werden. Die Entdeckung eines Helium-Weißen-Zwergs, der nicht der harte Kern eines sonnenähnlichen Sterns ist, sondern ein gasförmiger erloschener Roter Zwerg, würde somit entweder die Sternenevolutionsmodelle oder die Urknall-Theorie widerlegen, da er entweder erstaunlich jung erloschen wäre oder das Universum deutlich älter sein müsste als gedacht. Ein solches Objekt bisher jedoch nicht gesichtet.
Die Entdeckung eines Helium-Weißen-Zwergs, der aus einem gasförmigen erloschenen Roten Zwerg entstanden ist, würde entweder die Sternenevolutionsmodelle oder die Urknall-Theorie widerlegen.
Allerdings ist das Fehlen alter Roter Zwerge, die nur aus Wasserstoff und Helium bestehen, und somit von den Anfängen des Universums stammen würden, ein großes Problem. Denn wenn ihre Lebensdauer tatsächlich so groß wäre, würde man Rote Zwerge jeden Alters entdecken können, einschließlich sehr alter Roter Zwerge, die seit der Anfangszeit des Universums existieren. Tatsächlich sind die bisher gefundenen Roten Zwerge erstaunlich reich an schweren Elementen, haben eine hohe Metallizität und sind somit, laut Urknallmodell, ziemlich jung. Wenn Rote Zwerge wirklich älter werden könnten als das Universum laut Urknallmodell, müssten wir auch Rote Zwerge mit sehr hohem Alter finden. Diese Roten Zwerge würden laut Urknallmodell entsprechend wenig oder gar keine Metalle enthalten. Das Fehlen dieser Objekte ist ein heiß diskutiertes Problem. (Bonfils 2005; Wenz 2019; Schlaufman et al. 2018; Parks 2023)
Aufgrund der hohen „Lebensdauer“ von Roten Zwergen müsste es Rote Zwerge geben, die nur aus Wasserstoff und Helium bestehen, – diese fehlen aber.
Außerdem wurden um ca. einen Faktor 100 weniger Braune Zwerge entdeckt als von Sternevolutionsmodellen vorhergesagt. Braune Zwerge sind Objekte, die kleiner als Rote Zwerge, jedoch deutlich schwerer als Gasplaneten wie der Jupiter sind. Sie können zwar nicht Wasserstoff zu Helium fusionieren, aber sie fusionieren Wasserstoff zu Deuterium (schwerem Wasserstoff). Diese kleinen, schwach leuchtenden Objekte müssten allgemein sehr häufig sein, weil kleine Sterne häufiger sind als große. Man versucht die fehlenden Braunen Zwerge damit zu erklären, dass Braune Zwerge sehr schwer zu beobachten sind, da sie nur wenig größer als der Jupiter sind und kaum leuchten.[23]
Es wurden um ca. einen Faktor 100 weniger Braune Zwerge entdeckt als von Sternevolutionsmodellen vorhergesagt.
Interessant wären ebenfalls Beobachtungen von Sternen, die sich jetzt gerade rasant verändern. Als Beispiel ist T Ursae Minor zu nennen. Dieser pulsierende Rote Riese hat sich laut Daten von Amateurastronomen in den letzten hundert Jahren nur wenig verändert. Vor 20 Jahren begannen sich die Schwingungen und damit die Helligkeitsschwankungen des Sterns plötzlich rasant zu verändern. Es wäre interessant zu beobachten, ob dieser Stern wirklich eine neue stabile Phase ansteuert und noch einige Jahrmillionen existieren kann, wie die Sternevolutionsmodelle vorhersagen. Wären Sterne aber deutlich kurzlebiger, als die Sternenevolutionsmodelle vorhersagen, könnte T Ursae Minor noch zu unseren Lebzeiten zur Supernova werden. Andere Sterne, die sich in den letzten Jahrzehnten stark verändert haben, sind zum Beispiel R Dorados, P Cygni oder Eta Carinae. (Molnár et al. 2019; Lamers et al. 1985)[24]
6. Fazit
Unabhängig davon, ob Sterne Jahrtausende, Jahrmillionen oder Jahrmilliarden für ihre Entwicklung brauchen, es ist in jedem Fall eine zu lange Zeit, um den Prozess vollständig beobachten zu können. Grundsätzlich ist die Reihenfolge der verschiedenen Entwicklungsschritte von Sternen durchaus plausibel. Wie lange sie aber für diese Phasen brauchen, kann nur mit Modellen berechnet werden und anhand von Sternhäufigkeiten im HR-Diagramm verifiziert werden.
Es gibt zurzeit zwei Hauptklassen von Modellen. Das eine ist das Standartsonnenmodell MESA, welches vor allem thermo- und hydrodynamische Gleichungen löst und mit dem hydrostatischen Equilibrium arbeitet. Die anderen sind die sogenannten helioseismologischen Modelle, mit denen anhand der Oszillationen der heutigen Sonne ihre Vergangenheit berechnet werden soll.
In beiden Modellen wird eine Entstehung der Sonne aus einer Gaswolke zugrunde gelegt, die unter ihrer Gravitation kollabiert ist. Während MESA die Masse, den Radius und die Helligkeit der Sonne einbezieht, konzentrieren sich die helioseismologischen Modelle auf die Schwingungen und das Magnetfeld. Diese Größen sind, sowie auch die Kernfusionsvorgänge im Inneren der Sonne und die Temperatur innen und außen, messbar. Hierbei helfen Neutrinos aus dem Sonnenkern und Spektralanalysen des Sonnenlichts. Auf diese Weise kann man auch die chemische Zusammensetzung der Sonnenoberfläche messen. Die innere chemische Zusammensetzung und die Opazitäten der verschiedenen chemischen Elemente, können wir hingegen bisher nicht messen.
Vereinfachungen wie das Ideale Gas spielen in den Berechnungen von MESA keine große Rolle. Das Nichtberücksichtigen der Rotation könnte hingegen problematisch sein, weil die Rotation den Sonnenzyklus verursacht und somit indirekt größeren Einfluss hat.
Im Gegensatz dazu benötigen die helioseismologischen Modelle Annahmen über die ursprüngliche Rotation und Oszillation der Sonne, die wir nicht überprüfen können.
Wenn wir von dem Schöpfungsbericht in der Bibel ausgehen (1. Mose 1,12-19), hatte die Sonne vom ersten Tag ihrer Erschaffung an die richtige Größe, Helligkeit und Temperatur, um pflanzliches Leben und anschließend auch tierisches und menschliches Leben auf der Erde zu ermöglichen (1. Mose 1,20-31). Dementsprechend hätte man bereits am 4. Schöpfungstag einen Stern vor sich gesehen, der sich laut Sternenevolutionsmodellen im stabilen Hauptreihenstadium befindet – und nicht in der instabilen und lebensfeindlichen Protosternphase, die laut Sternenevolutionsmodellen zuvor erfolgt sein müsste. Somit kann man von einem „geschaffenen Alter“ oder „Startalter“ der Sonne auszugehen (ggf. auch in Form einer Zeitrafferschöpfung oder einer alternativen Zeitkonvention; vgl. Trüb 2011; 2022), der ihrem Zweck entspricht, lebensfreundliche Strahlungsintensität und Wellenlängen auf die Erde zu senden.[25] Diese Strahlung muss zu diesem Zeitpunkt bereits auf dem Weg zur Erde gewesen sein (der übrigens ungefähr 8 Minuten und 20 Sekunden dauert), und hätte nicht erst mühsam den Kern verlassen müssen. Daher stellt sich die Frage, wie der biblische Schöpfungsbericht in Beziehung zu setzen ist mit radiometrischen Datierungsmethoden von Planetengesteinen und Meteoriten in unserem Universum.
Die Entwicklungen der Sonnenschwingungen liefern für die Sonne viele unterschiedliche Altersberechnungen zwischen 4 und 12 Milliarden Jahren. Da hierbei aber auch der Radius und die Helligkeiten der simulierten Sonne sehr unterschiedlich sind, könnten viele davon für unsere Sonne ausgeschlossen werden. Auch die Modelle einer rotierenden Sonne bieten kein Indiz für ein junges Alter, da sich die Helligkeit der Sonne gemäß dieser Modelle im Laufe der Zeit stark verändert hat.
Interessant sind besonders die chemische Zusammensetzung und die Opazität der Sonne. Es steht noch keine Methode zur Verfügung, um zu überprüfen, ob die Sonne wirklich chemisch homogen ist. Allerdings werden zukünftige Messungen der Opazität viele neue Modelle liefern. Die im Labor gemessenen Kenntnisse über Eisen haben damit alle bisherigen Theorien widerlegt – und so könnte es auch bei anderen chemischen Elementen sein. Und mit Veränderungen in der Opazität könnte das Licht schneller nach außen gelangen als die berechneten 10.000 bis 170.000 Jahre.
Das Fehlen von alten Roten Zwergen als auch der Mangel an Braunen Zwergen stellt die Wissenschaft vor ein Rätsel. Zudem könnten uns Beobachtungen von Sternen, die sich jetzt gerade schnell verändern, wie auch das aufkommende Feld der Stellarseismologie viele neue Daten für neue Modelle liefern.
Am Ende bleibt unsere Erkenntnis immer Stückwerk und wir können uns weiterhin auf spannende Messergebnisse und Simulationen freuen.
7. Literatur
Agostini M et al. (2017) Limiting neutrino magnetic moments with Borexino Phase-II solar neutrino data. Phys. Rev. D 96, 091103, doi: https://doi.org/10.1103/PhysRevD.96.091103.
Anandaram MN (2014) On the Tachocline Zone Location in the Sun, the Luminosity Transport time scale, the Rotational Inertia and their Time Variation in Standard Solar Evolution Models. Mapana J. Sci. 14, 49–76, doi: 10.12723/mjs.28.4.
Badnell NR et al. (2005) Up-dated opacities from the Opacity Project. Mon. Not. Roy. Astron. Soc. 360, 458–464, https://doi.org/10.1111/j.1365-2966.2005.08991.x.
Bahcall JN & Ulmer A (1996) The temperature dependence of solar neutrino fluxes. Phys. Rev. D53, 4202–4210, https://doi.org/10.1103/PhysRevD.53.4202.
Bailey JE et al. (2015) A higher-than-predicted measurement of iron opacity at solar interior temperatures. Nature 517, 56–59, https://doi.org/10.1038/nature14048.
Bellerive A (2004) Review of Solar Neutrino Experiments. Int. J. Mod. Phys. A19, 1167–1179, https://doi.org/10.1142/S0217751X04019093; hier verfügbar: arXiv:hep-ex/0312045v1.
Bertazzo S et al. (2015) Fibres and cellular structures preserved in 75-million–year-old dinosaur specimens. Nat. Commun. 6, 7352, https://doi.org/10.1038/ncomms8352.
Bétrisey J (2024) Imprint of the magnetic activity cycle on solar asteroseismic characterisation based on 26 years of GOLF and BiSON data. A&A 688, L17, https://doi.org/10.1051/0004-6361/202451365.
Binder H (2020) Elastische Gewebereste, Zellbausteine und Proteinfragmente in Dinosaurier-Fossilien. W+W-Onlineartikel vom 27.04.2020, https://www.wort-und-wissen.org/artikel/elastische-gewebereste-zellbausteine-und-proteinfragmente-in-dinosaurier-fossilien/.
Bonanno A & Fröhlich HE (2015) A Bayesian estimation of the helioseismic solar age. A&A 580, A130, https://doi.org/10.1051/0004-6361/201526419.
Bonfils X (2005) Metallicity of M dwarfs. I. A photometric calibration and the impact on the mass-luminosity relation at the bottom of the main sequence. A&A 442, 635–642, doi: 10.1051/0004-6361:20053046.
Capelo D & Lopes I (2020) The impact of composition choices on solar evolution: age, helio- and asteroseismology, and Neutrinos. Monthly Notices of the Royal Astronomical Society 498, 1992–2000, https://doi.org/10.1093/mnras/staa2402.
CBSNews.com (2000) Bacteria, 250 Million Years Young, vom 18.10.2000, https://www.cbsnews.com/news/bacteria-250-million-years-young/.
Charbonneau P (2014) Solar Dynamo Theory. Annu. Rev. Astron. Astrophys. 52, 251–290, https://doi.org/10.1146/annurev-astro-081913-040012.
Christensen-Dalsgaard J, Gough DO & Thompson MJ (1991) The Depth of the Solar Convection Zone. ApJ. 378, 413, doi: 10.1086/170441.
Ehrmann A (2019) Alter und Prozesse mit Zeitrelevanz bei Sternen und Planeten. 33. Fachtagung Physik & Kosmologie der SG Wort und Wissen 2019.
Farag E et al. (2020) On Stellar Evolution in a Neutrino Hertzsprung–Russell Diagram. ApJ 893, 133, doi: 10.3847/1538-4357/ab7f2c.
Gizon L & Birch AC (2012) Helioseismology challenges models of solar convection. PNAS 109, 11896–11897, https://doi.org/10.1073/pnas.1208875109.
Haxton WC (1995) The solar neutrino problem. Ann. Rev. Astron. Astrophys. 33, 459–503, doi: https://doi.org/10.1146/annurev.aa.33.090195.002331.
Hoarty DJ et al. (2019) A proposal to measure iron opacity at conditions close to the solar convective zone-radiative zone boundary. High Energy Density Physics 32, 70–76, https://doi.org/10.1016/j.hedp.2019.05.003.
Jermyn AS et al. (2023) Modules for Experiments in Stellar Astrophysics (MESA): Time-Dependent Convection, Energy Conservation, Automatic Differentiation, and Infrastructure. ApJS 265, 15, doi: 10.3847/1538-4365/acae8d.
Kotulla M (2020) Geologie. Loseblattsammlung. Zusammenstellung der gesamten Loseblatt-Sammlung. W+W-Onlineartikel vom Oktober 2020, https://www.wort-und-wissen.org/wp-content/uploads/Gueltigkeit-und-Grenzen-geologischer-Zeitbestimmung.pdf.
Lamers HJGLM, Korevaar P & Cassatella A (1985) The ejection of shells in the stellar wind of the hypergiant P Cygni (B1 Ia/+/). A&A 49, 29–40, https://adsabs.harvard.edu/full/1985A%26A…149…29L.
Langer N & Kudritzki RP (2014) The spectroscopic Hertzsprung-Russell diagram. A&A 564, A52, https://doi.org/10.1051/0004-6361/201423374.
Lodders K, Bergemann M & Palme H (2025) Solar System Elemental Abundances from the Solar Photosphere and CI-Chondrites. Space Sci. Rev. 221, 23, https://doi.org/10.1007/s11214-025-01146-w.
MESA HUB (2022) https://github.com/MESAHub/mesa/blob/9fc77aacaa7f3a1f08380ce7af1a4f2d5c081e3c/star/test_suite/ppisn/src/run_star_extras.f90#L460 (Stand: 11.6.2024).
Mitalas R & Sills KR (1992) On the Photon Diffusion Time Scale for the Sun. ApJ 401, 759, doi: 10.1086/172103.
Molnár L, Joyce M & Kiss L (2019) Stellar Evolution in Real Time: Models Consistent with Direct Observation of Thermal Pulse in T Ursae Minoris. arXiv:1905.00597 [astro-ph.SR], https://doi.org/10.3847/1538-4357/ab22a5.
Park TS (2001) Parameter-Free Calculation of the Solar Proton Fusion Rate in Effective Field Theory, arXiv:nucl-th/0106025, https://doi.org/10.48550/arXiv.nucl-th/0106025.
Parks J (2023) Astronomers spot one of the oldest stars in the entire universe, vom 07.11.2023, https://www.astronomy.com/science/astronomers-spot-one-of-the-oldest-stars-in-the-entire-universe/.
Paxton B et al. (2013) Modules for experiments in stellar astrophysics (MESA): Planets, oscillations, rotation, and massive stars. ApJS 208, 1, 4, https://doi.org/10.1088/0067-0049/208/1/4.
Paxton B et al. (2018) Modules for Experiments in Stellar Astrophysics (MESA): Convective Boundaries, Element Diffusion, and Massive Star Explosions. ApJS 234, 34, doi: 10.3847/1538-4365/aaa5a8.
Russel R (2007) The Multispectral Sun, vom 18.04.2007, https://www.windows2universe.org/sun/spectrum/multispectral_sun_overview.html.
Salmon S et al. (2021) Standard solar models: a perspective from updated solar neutrino fluxes and the gravity-mode period spacing. A&A 651, A106, https://doi.org/10.1051/0004-6361/202140769.
Schlaufman KC, Thompson IB & Casey AR (2018) An ultra metal-poor star near the hydrogen-burning limit. ApJ 867.2 (2018): 98, https://doi.org/10.48550/arXiv.1811.00549.
Schwarzschild M, Howard R & Härm R (1957) Inhomogeneous Stellar Models. V. a. Solar Model with Convective Envelope and Inhomogeneous Interior. ApJ 125, 233, doi: 10.1086/146297.
Science Education through Earth Observation for High Schools (SEOS) Understanding Spectra from the Earth (seos-project.eu), https://seos-project.eu/earthspectra/earthspectra-c02-p12.html (Stand 11.6.2024).
Smirnov OY et al. (2016) Measurement of Solar pp-neutrino flux with Borexino: results and implications. J. Phys. Conf. Ser. 675, 012027, doi: 10.1088/1742-6596/675/1/012027.
Song N et al. (2018) Helioseismic and neutrino data-driven reconstruction of solar properties. Monthly Notices of the Royal Astronomical Society 477, 1397–1413, https://doi.org/10.1093/mnras/sty600.
Trüb P (2022) Licht, Raum, Zeit. Warum sehen wir das Licht entfernter Galaxien? | Dr. Peter Trüb, vom 20.06.2022, https://www.youtube.com/watch?v=shjIeTlvSJY.
Trüb P (2011) Die Konvention der Lichtkegel-Gleichzeitigkeit – Eine Lösung für das Problem langer Lichtlaufzeiten. W+W-Onlineartikel vom 30.06.2011, https://www.wort-und-wissen.org/artikel/die-konvention-der-lichtkegel-gleichzeitigkeit-eine-loesung-fuer-das-problem-langer-lichtlaufzeiten/.
Turck-Chieze S et al. (2010) Seismic and dynamical solar models i-the impact of the solar rotation history on neutrinos and seismic indicators. APJ 715, 1539–1555, https://doi.org/10.1088/0004-637X/715/2/1539.
Vinyoles N (2017) A New Generation of Standard Solar Models. ApJ 835, 202, doi: 10.3847/1538-4357/835/2/202.
Wang H et al. (2023) Evolutionary tracks of massive stars with different rotation and metallicity in neutrino H–R diagram. Monthly Notices of the Royal Astronomical Society 526, 4335–4344, https://doi.org/10.1093/mnras/stad3071.
Wenz J (2019) Four Types of Stars That Will Not Exist for Billions or Even Trillions of Years, vom 18.02.2019, https://www.smithsonianmag.com/science-nature/four-types-stars-will-not-exist-billions-or-even-trillions-years-180971299/.
Weymann R (1957) Inhomogeneous Stellar Models.VI. an Improved Solar Model with the Carbon Cycle Included. ApJ 126, 208, https://adsabs.harvard.edu/pdf/1957ApJ…126..208W.
Wittkowski M (2004) Fundamental stellar Parameters. arXiv:astro-ph/0412519, https://doi.org/10.48550/arXiv.astro-ph/0412519. Erschienen in: Bulletin de la Socié Royale des Sciences de Liège – Vol. 74, 1-2-3, 2005, 165–181.
Yusof N et al. (2021), The neutrino emission from thermal processes in very massive stars in the local universe, arXiv:2103.07069v1 [astro-ph.HE], https://doi.org/10.1093/mnras/stab762.
[1] Best practices — MESA main documentation (mesastar.org), https://docs.mesastar.org/en/latest/using_mesa/best_practices.html (Stand 11.6.2024).
[2] Best practices — MESA main documentation (mesastar.org), https://docs.mesastar.org/en/latest/using_mesa/best_practices.html (Stand 11.6.2024)
[3] Best practices — MESA main documentation (mesastar.org), https://docs.mesastar.org/en/latest/using_mesa/best_practices.html (Stand 11.6.2024)
[4] Best practices — MESA main documentation (mesastar.org), https://docs.mesastar.org/en/latest/using_mesa/best_practices.html (Stand 11.6.2024).
[5] Best practices — MESA main documentation (mesastar.org), https://docs.mesastar.org/en/latest/using_mesa/best_practices.html (Stand 11.6.2024).
[6] https://en.wikipedia.org/wiki/Brown_dwarf (Stand 11.6.2024).
[7] https://de.wikipedia.org/wiki/Meteorit (Stand 11.6.2024).
[8] https://de.wikipedia.org/wiki/Titan_(Mond) (Stand 11.6.2024).
[9] https://en.wikipedia.org/wiki/Frost_line_(astrophysics) (Stand 11.6.2024).
[10] https://en.wikipedia.org/wiki/Frost_line_(astrophysics) (Stand 11.6.2024).
[11] https://en.wikipedia.org/wiki/Solar_constant; https://en.wikipedia.org/wiki/Sunlight, https://en.wikipedia.org/wiki/Sunlight (Stand jeweils 11.6.2024).
[12] https://en.wikipedia.org/wiki/Solar_constant; https://en.wikipedia.org/wiki/Sunlight, https://en.wikipedia.org/wiki/Sunlight (Stand jeweils 11.6.2024).
[13] https://www.leifiphysik.de/astronomie/sonne/grundwissen/aufbau-der-sonne (Stand 11.6.2024).
[14] In diesem Jahr habe ich während meiner Bachelorarbeit vergeblich nach Flares, Sonnenstürmen und Flecken gesucht.
[15] https://en.wikipedia.org/wiki/Solar_neutrino; https://en.wikipedia.org/wiki/Solar_neutrino_problem#Proposed_solutions (Stand jeweils 22.6.2024).
[16] https://de.wikipedia.org/wiki/Neutrinoobservatorium; https://en.wikipedia.org/wiki/Solar_neutrino (Stand jeweils 11.6.2024).
[17] https://en.wikipedia.org/wiki/Solar_neutrino (Stand 11.6.2024).
[18] https://en.wikipedia.org/wiki/Solar_neutrino (Stand 11.6.2024).
[19] https://en.wikipedia.org/wiki/Sunlight; Science Education through Earth Observation for High Schools (SEOS) Understanding Spectra from the Earth (seos-project.eu), https://seos-project.eu/earthspectra/earthspectra-c02-p12.html (Stand 11.6.2024).
[20] https://en.wikipedia.org/wiki/Sunlight; Science Education through Earth Observation for High Schools (SEOS) Understanding Spectra from the Earth (seos-project.eu), https://seos-project.eu/earthspectra/earthspectra-c02-p12.html (Stand 11.6.2024).
[21] https://en.wikipedia.org/wiki/Brown_dwarf; https://de.wikipedia.org/wiki/Meteorit (jeweils Stand 11.6.2024).
[22] https://de.wikipedia.org/wiki/Meteorit; https://de.wikipedia.org/wiki/Mondkrater (Stand jeweils 11.6.2024).
[23] https://en.wikipedia.org/wiki/Brown_dwarf (Stand 11.6.2024); Leipniz-Institut für Astrophysik Potsdam (2016) The Missing Brown Dwarfs, vom 08.04.2016, https://www.aip.de/en/news/the-missing-brown-dwarfs/.
[24] https://en.wikipedia.org/wiki/R_Doradus (Stand 11.6.2024).
[25] 1. Mo 1,14 „Und Gott sprach: Es werden Lichter an der Ausdehnung des Himmels, um den Tag von der Nacht zu scheiden, und sie seien zu Zeichen und zur Bestimmung von Zeiten und Tagen und Jahren; 15 und sie seien zu Lichtern an der Ausdehnung des Himmels, um auf die Erde zu leuchten! Und es wurde so. 16 Und Gott machte die zwei großen Lichter: das große Licht zur Beherrschung des Tages, und das kleine Licht zur Beherrschung der Nacht – und die Sterne. 18 und dass sie am Tag und in der Nacht herrschen und das Licht von der Finsternis scheiden. Und Gott sah, dass es gut war.“ (1. Mose 1,14-18; ELB CSV; Hervorh. hinzugef.)